Rayleigh/Numerical damping

[Sarah]

I was doing a test simulation of a mesh(tetras) with the corners constrained and then was looking at the displacement of the bottom facenode of the Mesh when applying gravity.

I’m using Eulerimplicit, a SparseLDLSolver and TetrahedronFEMForceField for the mesh.

Funny enough as I decreased the time step from 0.01 to 0.0001 the node tended to oscillate more before coming to a stable position.
See this zoomed in image (t=0.0001 ends up stabalizing at a larger value of t):
Displacement of FaceNode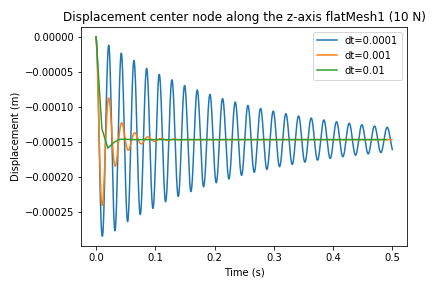

It seems as though this could be related to a form of numerical damping (possibly from the EulerImplicitSolver, but have Rayleigh stiffness and mass both set to 0). Is there any other numerical damping involved in the system?

I’m thinking I will use a iterative solver instead of a direct one (CGLinearSolver perhaps), but am guessing this oscilation is related to the EulerImplicitSolver and not the SparseLDLSolver.

Are there any other possible sources of numerical damping that could be causing this?

[Sarah]

Here is the link to the image:
Displacement

[Hugo]

Hi @sarah

Interesting point.
If you did set the Rayleigh damping (all parameters) to zero and you did not add any damping forcefield in the scene, there is no numerical damping supposed to act.

SparseLDLSolver is a very good solution, it will find the exact solution to the linear system.

Could you tell me which mass are you using?
Did you define some plasticity?
Is there any other forcefield acting in the scene ?

Best,

Hugo

[Sarah]

Hi Hugo,

I thought I had responded earlier, but for some reason my posts weren’t coming through as they were being recognized as spam (but got that figured out now!).

To answer some of your questions, I was using UniformMass, but see the same behaviour although with a larger displacement for the DiagonalMass. I don’t have any plasticity set, am just using the TetrahedronFEMForceField and besides gravity(set to 10m/s^2 for simplicity) have no other forces acting on the scene. The total mass of the slab is 0.1kg, all my units are in SI. Furthermore, in the graph it should say “(1N)”.

Here is my code. I’ve found that when setting the rayleighMass and the rayleighStiffness to 0.0063 the system is critically damped for dt=0.001 when using mesh, flat2 which is a little coarser then the one from the previous picture, but gives very similar results.
Here is the code using flat2. With the link to flat2.vtk

flat2.vtk

import Sofa
import os
#Location of Meshes and objects
path = 'details/data/mesh/'
volumeMesh='flat2.vtk'

def createScene(rootNode):

	################# ROOTNODE #################

	rootNode.findData('gravity').value='0 0 -10'
	rootNode.findData('dt').value='0.001'
	rootNode.createObject('RequiredPlugin', name='soft', pluginName='SoftRobots')
	rootNode.createObject('RequiredPlugin', name='SofaSparseSolver', pluginName='SofaSparseSolver')
	rootNode.createObject('DefaultAnimationLoop')

	################# flat #################
	#Create the flat node, load, store and build the mesh into a Mechanical Object
	flat = rootNode.createChild('flat')
	flat.createObject('MeshVTKLoader', name='loader', filename= path + volumeMesh)
	flat.createObject('Mesh', src='@loader', name='container')
	flat.createObject('MechanicalObject', name='tetras', template='Vec3d', showObject='true', scale='1')	
	flat.createObject('UniformMass', totalMass='0.1')
	flat.createObject('TetrahedronFEMForceField', template='Vec3d', name='FEM', method='large', poissonRatio='0.49', youngModulus='1000000')
	
	flat.createObject('EulerImplicit', name='odesolver', rayleighStiffness="0.00", rayleighMass="0.00")
	flat.createObject('SparseLDLSolver', name='directSolver')

	################# STATIC BOX #################
	flat.createObject('BoxROI', name='boxROI', box='0 0 0 0.01 0.01 0.01 0 0.09 0 0.01 0.1 0.01 0.09 0 0 0.1 0.01 0.01 0.09 0.09 0 0.1 0.1 0.01', drawBoxes=True)
	flat.createObject('FixedConstraint', name='FixedConstraint', indices='@boxROI.indices')

	################# MONITOR #################
	flat.createObject('Monitor', name="monitor-displacement-faceNode", indices="45", template="Vec3d",
		showPositions=True, PositionsColor="1 0 1 1", ExportPositions=True, 
		showVelocities=False, VelocitiesColor="0.5 0.5 1 1", ExportVelocities=False, 
		showForces=True, ForcesColor="0.8 0.2 0.2 1", ExportForces=True, 
		showTrajectories=False, TrajectoriesPrecision="0.1", TrajectoriesColor="0 1 1 1", sizeFactor="1")

Also when I used the CGLinearSolver, for each order of the timestep two oscillations occured; one that was damped and one that remained fluctuating. The latter had a period which was proprtional to the size of the timestep (7 sec, 0.7 sec and 0.07 sec[0.01, 0.001, 0.0001 respectively]), this oscillation however arises because of the itterative solver and doesn’t explain the previous image.

Would be curious to hear your thoughts on where this oscillation could be coming from. Could there be some other form of numerical damoing involved?

[Hugo]

Hi @sarah

First of all, thank you, you made me re-discover the Monitor + Gnuplot feature. Quite convenient when you want to shortly analyze and visualize the behavior of a body in the simulation.

Regarding your question, I needed a bit of time to gather the appropriate answer.
The Euler scheme is an order 1 (in time) integration scheme and it is known to be a dissipative scheme. Moreover, only one Newton step is performed in the EulerImplicit, which might harm the energy conservation. Then, why using such a scheme? SOFA is a framework aiming at interactive simulations. For this purpose, dissipative schemes are very appropriate.

You can see that activating the trapezoidalScheme option of the Euler implicit scheme, makes it less dissipative. This is due to the fact that the trapezoidal rule increases the order of the time integration. And higher order schemes are known to be less dissipative.

NewmarkImplicitScheme has the same trapezoidal approach, and, it makes several Newton step. There, almost no dissipation is noticed.

I hope this help.
Best wishes,

Hugo

[Sarah]

Hi Hugo,

This is very interesting. I can imagine that the dissipative nature of Euler scheme is causing this.. I applied these different solvers and got the results as shown in the image. Newmark doesn’t seem to apporximate the situation well. The Euler with trapezoidalScheme does better, but isn’t more dissipative…

In light of this however it does make sense that finer time steps would have less dissipation, as in the image in the initial post. But it is still rather puzzeling.

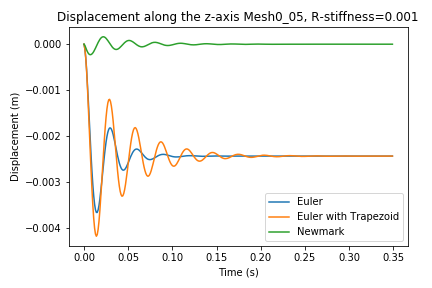
(in this simulation I used a rayleigh stiffness of 0.001 and mass of 0, this as when both set to 0 the trapezoidal scheme didn’t give stable results.)

Many thanks!

Sarah

[Hugo]

Hi @sarah

Good to see your further investigations!
Could you explain why you used a non-zero Rayleigh stiffness? this will cause damping.
Did you set this Rayleigh coefficient in the integration scheme?

Best,

Hugo

PS: what was exactly the question btw?

[Sarah]

Hi @Hugo,

I added a non-zero Rayleigh stiffness as else using the trapezoidal scheme my object completely lost its shape, it became unstable. Upon slight damping (as I set in the integration scheme it remained stable). I found this useful link, in particualr the second comment about the EulerImplicit (I’m still rather new to FEM) and it makes sense that a smaller time step will lead to less dissipation and thus a higher amplitude. But what about the frequency? The trapezoidal scheme seems to make sense, but the Newmark still puzzles me would think it would show results similar to both the finer time step as well as to the trapezoidal scheme.

–Much have the question has been answered 🙂
–There are still remaining questions I have:

1. Mainly is the higher frequency at a finer timestep also resulting directly from the ImplicitEuler?
2. And could there be any particualr reason that the Newmark is causing such a different response?

Hope that is clear. Thanks for the tips and ideas!

Kind regards,

Sarah

[Hugo]

Hi @sarah

Thanks for the interesting link!
For your information a BDF2 scheme has already been implemented. One is available here: ExplicitBDFSolver

If you want to analyze this dissipation effect, clearly no additional damping should be set up. Otherwise the interpretation will be complicated. I need some more time to look at your scene. Let me get back to you asap.

Best,

Hugo

[Author]

Posts